前面兩章了解模型概念與知識，今天終於來到了Q-learning的學習了！不然都說人工智慧人工智慧的，就讓我們來了解Q-learning到底智不智慧XD

Q-更新

今天我們換回馬力歐的例子，假設正在玩馬力歐，馬力歐走到小烏龜前面，來到緊張刺激的瞬間：
馬力歐看到小烏龜近在幾公分(輸入state1)，斷然決定平行直走撞上小烏龜(reward,state2)，遊戲結束(terminate)，藉由這三個值我們就可做Q更新。
先介紹兩個Q方法：

1. Q估計，就之前介紹的，估計state、action的值。
2. Q現實：Q現實是，當下獎懲加，衰減值乘下個狀態的最大值。

只要想想Q值都是由預想中每個連貫最大值組成[Day06 Q-value章節]，其實Q估計跟Q現實理想中就是要一致的值。我們會讓兩個值相減取均方差，再做反向傳播，神經網路就被更新囉！至於n就
等同是batch_size的數量哩！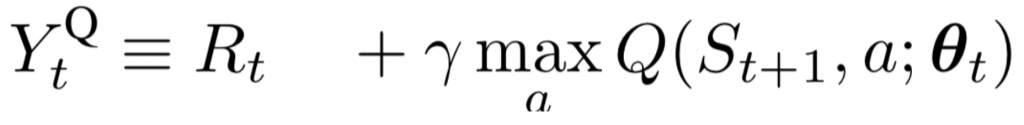

target-net：Q現實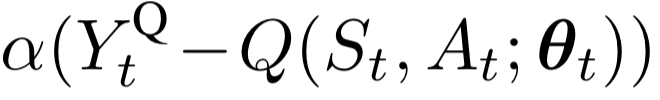

括號是Q現實減Q估計，α是學習率
或許有些讀者不太了解均方差，均方差也是L2跟Mean-Square Error，簡單來說差值怕有負的，讓值平方後就沒這問題了，把這些值加總除樣本數，最後就用梯度下降讓值逼近為零(收斂)。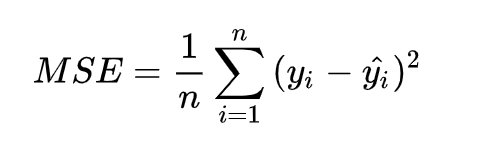

terminate reward

如果已到最後的state，觸發了episode結束的條件(例如踩到烏龜)，那最後的Q估計呢怎辦？難道是直接估計下輩子state嗎XD？nono下輩子已經是新的回合(episode)了，最後的Q估計不會包含下個Q現實，而僅有reward。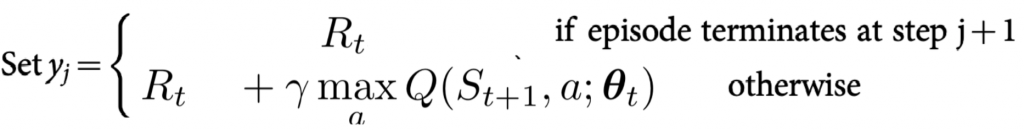

最後的reard相當重要，有些遊戲是到最終才給正的reward，假設你都沒走到最終，q-value很難更新，所以有些學習方法會先給一些好的樣本，例如模仿學習，讓你先學到些好樣本，對於開頭跑個幾萬次無頭緒來說，訓練會快上許多。

結語

回應開頭你們覺得AI很智慧嗎？我不認為XD 但讓我覺數學是偉大的。Q-learning印照著某些人生哲學與特性，但脫離抽象概念能用數學去表現，並且成功運行在某些領域上，這個過程很感動，要靠著許多人不斷研究跟實驗。好哩最核心的部分已經過去了，接下來再補充剩下Q-learning的概念與方法，大家明天見拉～